Local Integrals of Motion in Quasiperiodic Many-Body Localized Systems
Abstract
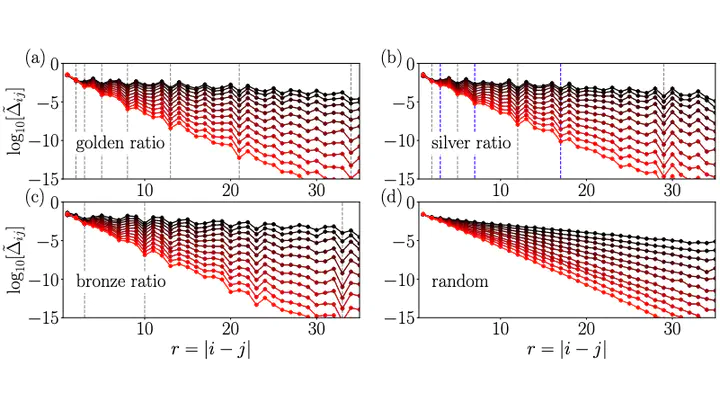
Local integrals of motion play a central role in the understanding of many-body localization in many-body quantum systems in one dimension subject to a random external potential, but the question of how these local integrals of motion change in a deterministic quasiperiodic potential is one that has received significantly less attention. Here we develop a powerful new implementation of the continuous unitary transform formalism and use this method to directly compute both the effective Hamiltonian and the local integrals of motion for many-body quantum systems subject to a quasiperiodic potential. We show that the effective interactions between local integrals of motion retain a strong fingerprint of the underlying quasiperiodic potential, exhibiting sharp features at distances associated with the incommensurate wavelength used to generate the potential. Furthermore, the local integrals of motion themselves may be expressed in terms of an operator expansion which allows us to estimate the critical strength of quasiperiodic potential required to lead to a localization/delocalization transition, by means of a finite size scaling analysis.