Local integrals of motion and the stability of many-body localisation in Wannier-Stark potentials

Abstract

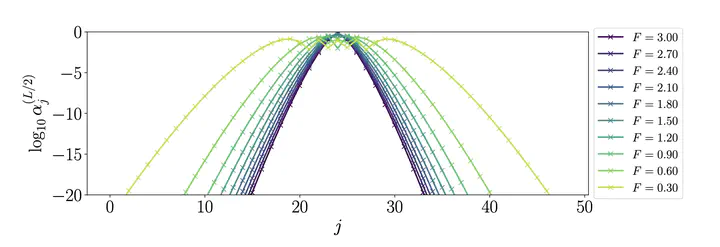
Many-body localisation in disordered systems in one spatial dimension is typically understood in terms of the existence of an extensive number of (quasi)-local integrals of motion (LIOMs) which are thought to decay exponentially with distance and interact only weakly with one another. By contrast, little is known about the form of the integrals of motion in disorder-free systems which exhibit localisation. Here, we explicitly compute the LIOMs for disorder-free localised systems, focusing on the case of a linearly increasing potential. We show that while in the absence of interactions, the LIOMs decay faster than exponentially, the addition of interactions leads to the formation of a slow-decaying plateau at short distances. We study how the localisation properties of the LIOMs depend on the linear slope, finding that there is a significant finite-size dependence, and present evidence that adding a weak harmonic potential does not result in typical many-body localisation phenomenology. By contrast, the addition of disorder has a qualitatively different effect, dramatically modifying the properties of the LIOMS.