Measuring out quasi-local integrals of motion from entanglement

Abstract

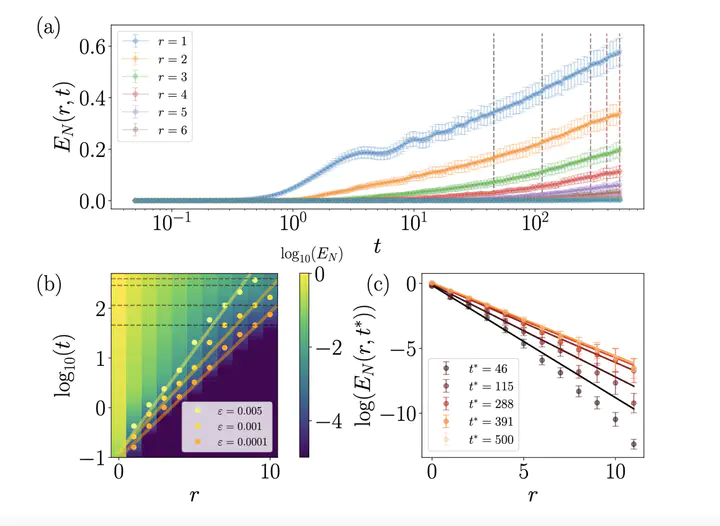
Quasi-local integrals of motion are a key concept underpinning the modern understanding of many-body localisation, an intriguing phenomenon in which interactions and disorder come together. Despite the existence of several numerical ways to compute them - and astoundingly in the light of the observation that much of the phenomenology of many properties can be derived from them - it is not obvious how to directly measure aspects of them in real quantum simulations; in fact, the smoking gun of their experimental observation is arguably still missing. In this work, we propose a way to extract the real-space properties of such quasi-local integrals of motion based on a spatially-resolved entanglement probe able to distinguish Anderson from many-body localisation from non-equilibrium dynamics. We complement these findings with a new rigorous entanglement bound and compute the relevant quantities using tensor networks. We demonstrate that the entanglement gives rise to a well-defined length scale that can be measured in experiments.