Disorder-induced spin-charge separation in the one-dimensional Hubbard model

Abstract

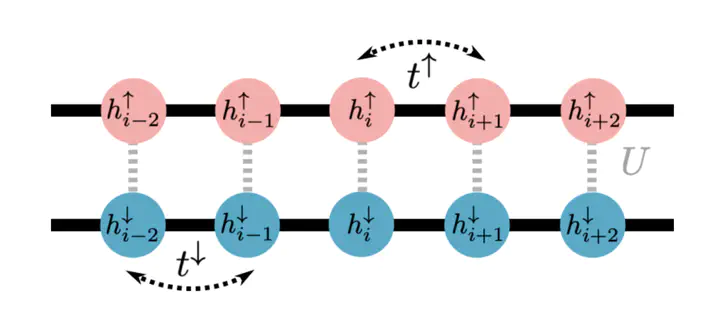
Many-body localization is believed to be generically unstable in quantum systems with continuous non-Abelian symmetries, even in the presence of strong disorder. Breaking these symmetries can stabilize the localized phase, leading to the emergence of an extensive number of quasilocally conserved quantities known as local integrals of motion, or l bits. Using a sophisticated nonperturbative technique based on continuous unitary transforms, we investigate the one-dimensional Hubbard model subject to both spin and charge disorder, compute the associated l bits and demonstrate that the disorder gives rise to a novel form of spin-charge separation. We examine the role of symmetries in delocalizing the spin and charge degrees of freedom, and show that while symmetries generally lead to delocalization through multiparticle resonant processes, certain subsets of states appear stable.